[알고리즘] 이진 탐색 (Binary Search)

1. 이진 탐색 (Binary Search) 이란?

• 탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법

이진 탐색의 이해 (순차 탐색과 비교하며 이해하기)

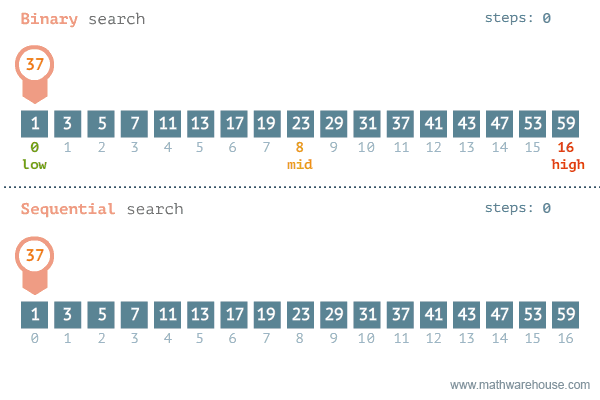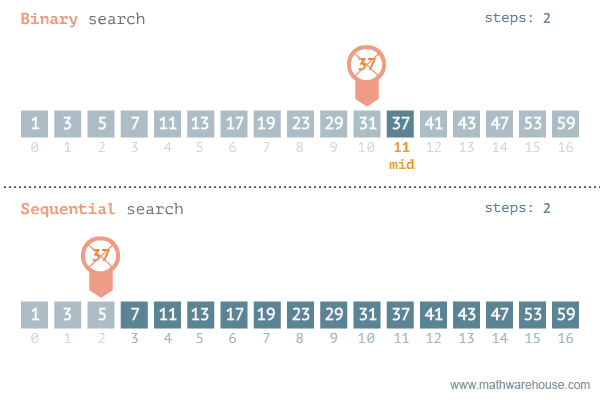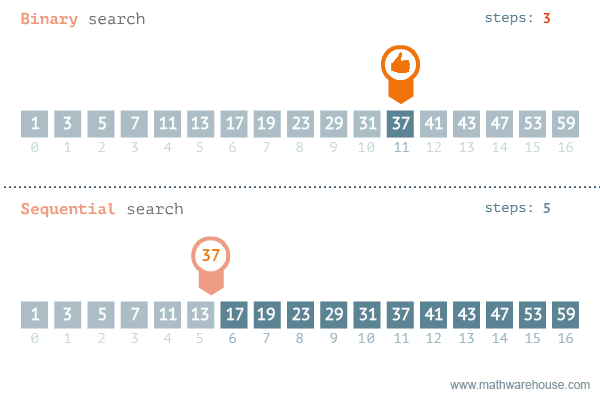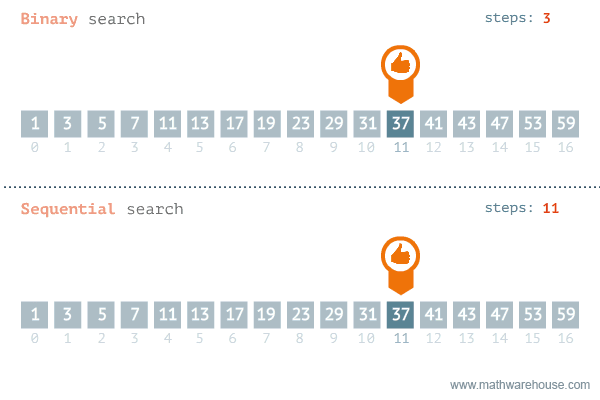
2. 분할 정복 알고리즘과 이진 탐색

분할 정복 알고리즘 (Divide and Conquer)

• Divide: 문제를 하나 또는 둘 이상으로 나눈다.
• Conquer: 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.

이진 탐색

• Divide: 리스트를 두 개의 서브 리스트로 나눈다.
• Conquer
  - 검색할 숫자(search) > 중간값(mid) 이면, 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
  - 검색할 숫자(search) < 중간값(mid) 이면, 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.

3. 프로그래밍 연습

어떻게 코드로 만들까?

이진 탐색은 데이터가 정렬되있는 상태에서 진행
데이터가 [2, 3, 8, 12, 20] 일 때,

• binary_search(data_list, find_data) 함수를 만들고
  - find_data는 찾는 숫자
  - data_list는 데이터 리스트
  - data_list의 중간값을 find_data와 비교해서,

  if find_data < data_list의 중간값:
    맨 앞부터 data_list의 중간까지 에서 다시 find_data 찾기
  elif data_list의 중간값 < find_data:
    data_list의 중간부터 맨 끝까지에서 다시 find_data 찾기
  else:
    data_list의 중간값은 find_data 인 경우로, return data_list 중간위치
  

알고리즘 구현

def binarySearch(dataList, search): # dataList 안에 검색하려는 대상(search)이 있으면 True, 없으면 False
    print(dataList) # binary search 과정 출력
    
    if len(dataList) == 1:
        if search == dataList[0]:
            return True
        else:
            return False
    if len(dataList) == 0: # 0일 경우는 없겠지만 방어코드
        return False
    
    mid = len(dataList)//2
    if search == dataList[mid]:
        return True
    else:
        if search > dataList[mid]:
            return binarySearch(dataList[mid:], search) # binarySearch의 뒷부분만 살리기
        else:
            return binarySearch(dataList[:mid], search) # binarySearch의 앞부분만 살리기

코드 이미지

테스트

4. 알고리즘 분석

---

💛 개인 공부 기록용 블로그입니다. 👻

맨 위로 이동하기